Embeddings from the Ground Up
This is the blog version of a talk of mine on embedding methods. It’s the main slides and what I would say in the talk.
Intended audience: Anyone interested in embedding methods. I don’t assume any prior knowledge, but we build up to advanced applications by the end, so even intermediate or advanced users can find useful information.
If you’re just interested in word embeddings and don’t mind some code, I recommend my previous post: https://wp.me/p9I3YF-5V
Embedding is the name we give to a collection of methods used to turn discrete objects into vectors of numbers. Normally this is used in the NLP context, turning words or sentences into vectors approximating them:

While this talk will use lots of NLP examples, we’ll go over wider uses of embedding methods.
Most introductory machine learning courses teach about the main subfields: supervised learning, reinforcement learning and unsupervised learning. The only domain normally taught in unsupervised learning is clustering, which misses much of the interesting work in that area.
The two big overlooked areas of unsupervised learning are embedding methods and the related subfield of self-supervised learning. Embedding exploded in popularity around 2013 with the introduction of word2vec which allowed training word embeddings on much larger corpus of text. This meant both that the embeddings were of higher quality (encoding much deeper semantic relationships) and having a vocabulary that captured most words used in regular use.
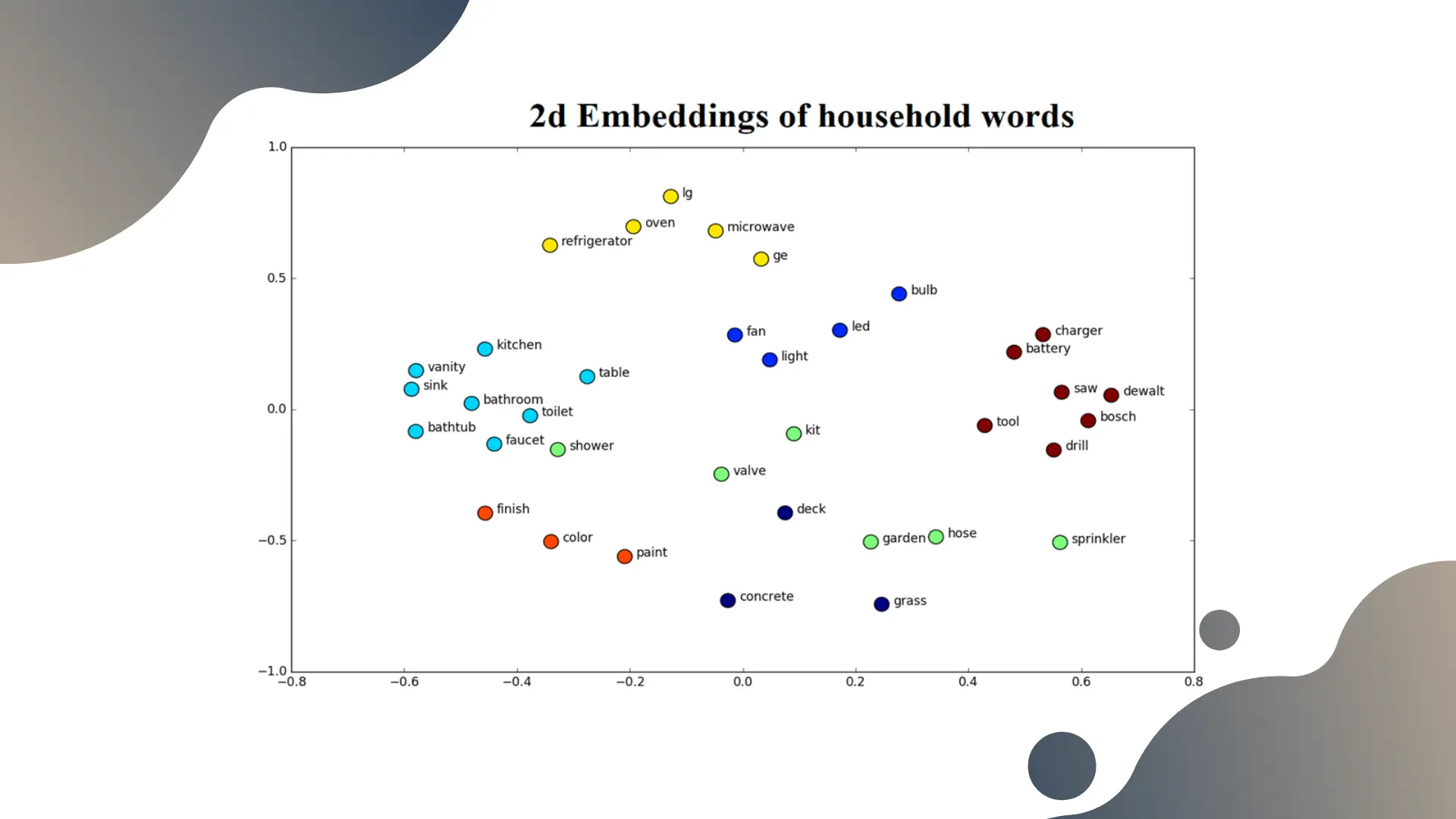
As we can see in this plot, the embeddings put the words on a coordinate system [footnote]Here, we reduced the 100-dimensional embeddings to 2 dimensions using T-SNE to plot them nicely[/footnote].
This unlocks for us the ability to “do math on words” – for instance in the plot above, we clustered the words and the resulting clusters seem to naturally represent types of home applications (kitchen use, bathroom, garage, etc.).
One famous use of word embeddings is “word algebra”, where we add and substract the vectors representing words and get intuitive results:

We would expect the result of Paris - France + Russia to be close to Moscow. We can try this in 3 lines of python with the helpful gensim library:
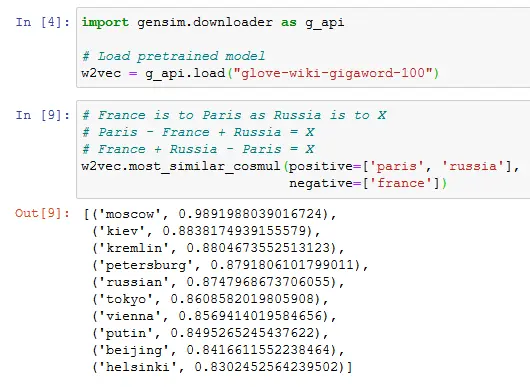
The result of the model includes the top related words, and their cosine distance from the result of our little equation.
The model not only gets the answer correctly, but the top 4 answers get sensible related concepts to the Russian capital city [footnote] Often, this sort of algebra degrades pretty quickly in quality outside of very obvious concepts, or with larger formulae[/footnote]
How are embeddings trained?
The fundamental assumption for most NLP work is the distributional hypothesis. The big corollary we put to work is that words appearing in a sentence together have a semantic relationship.
The easiest way to exploit this is to take a corpus of text, and transform it into a matrix where each column represents a word, and each row a sentence. Then each entry in the matrix indicates if the word appears in the matrix. This is called the bag of words model.
With a bit of linear algebra [footnote] Multiply the bag of words matrix by its transpose [/footnote] we can transform this model to a symmetric “co-occurence matrix” with words on the rows and columns. This new matrix keeps the count of how often words appear together in sentences. The diagonal of the symmetric word co-occurence matrix tracks how often the word appears overall in our text corpus.
(Code for these basic methods is in my word embeddings introduction post)
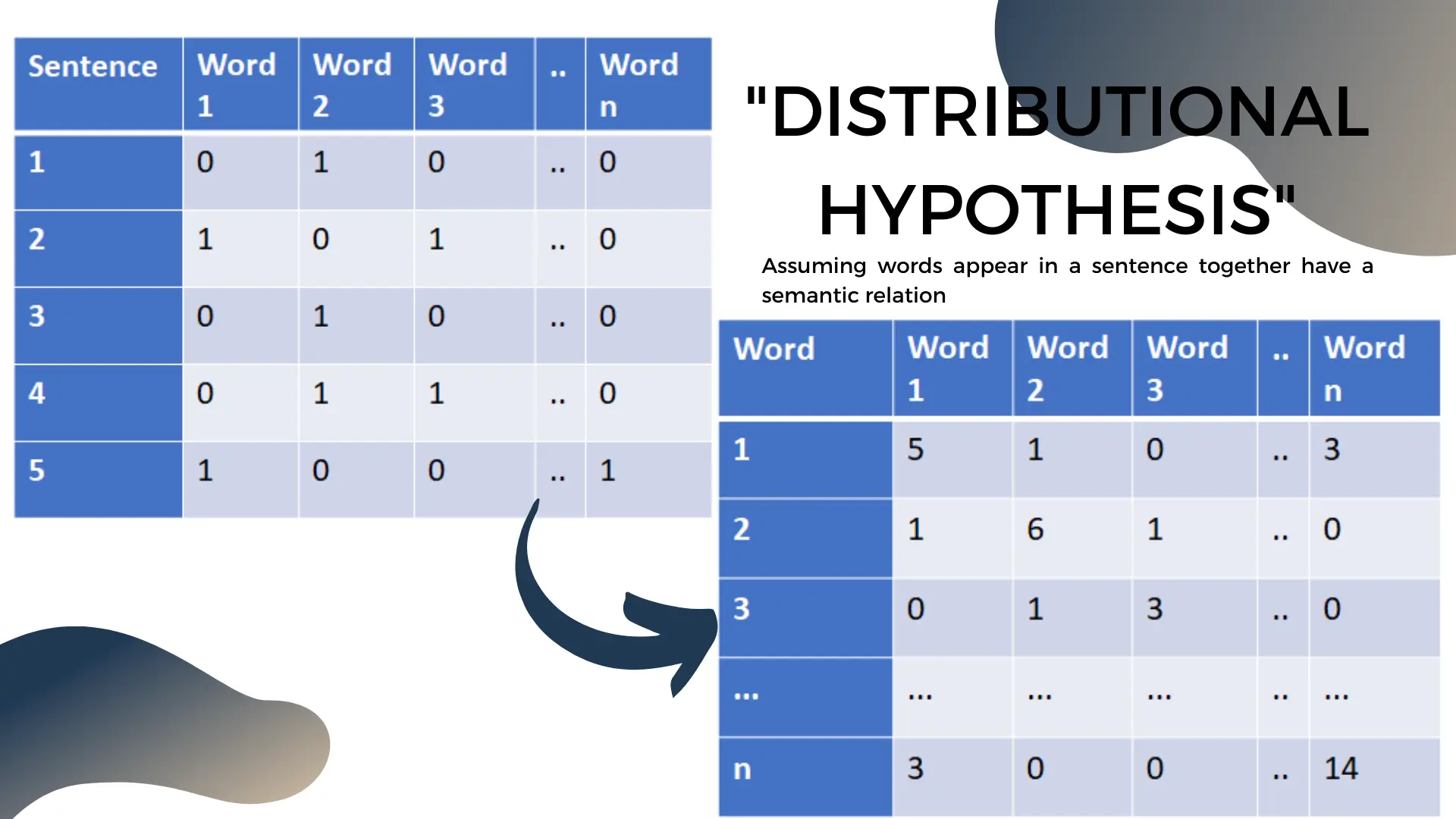
The word co-occurence matrix is an important object to understand. It’s already a word embedding model by itself: for any word, the vector of numbers in the associated row is an embedding. The only problem with it is is the sheer size of this matrix makes it hard to work with at scale [footnote] Word embedding models are often trained on all the text in wikipedia. The matrix will have millions of rows and columns, making linear algebra operations cumbersome or impossible[/footnote].
You should think of the word matrix as both a matrix and a mathematical graph. The matrix and the graph are the same mathematical object, but in different representation.
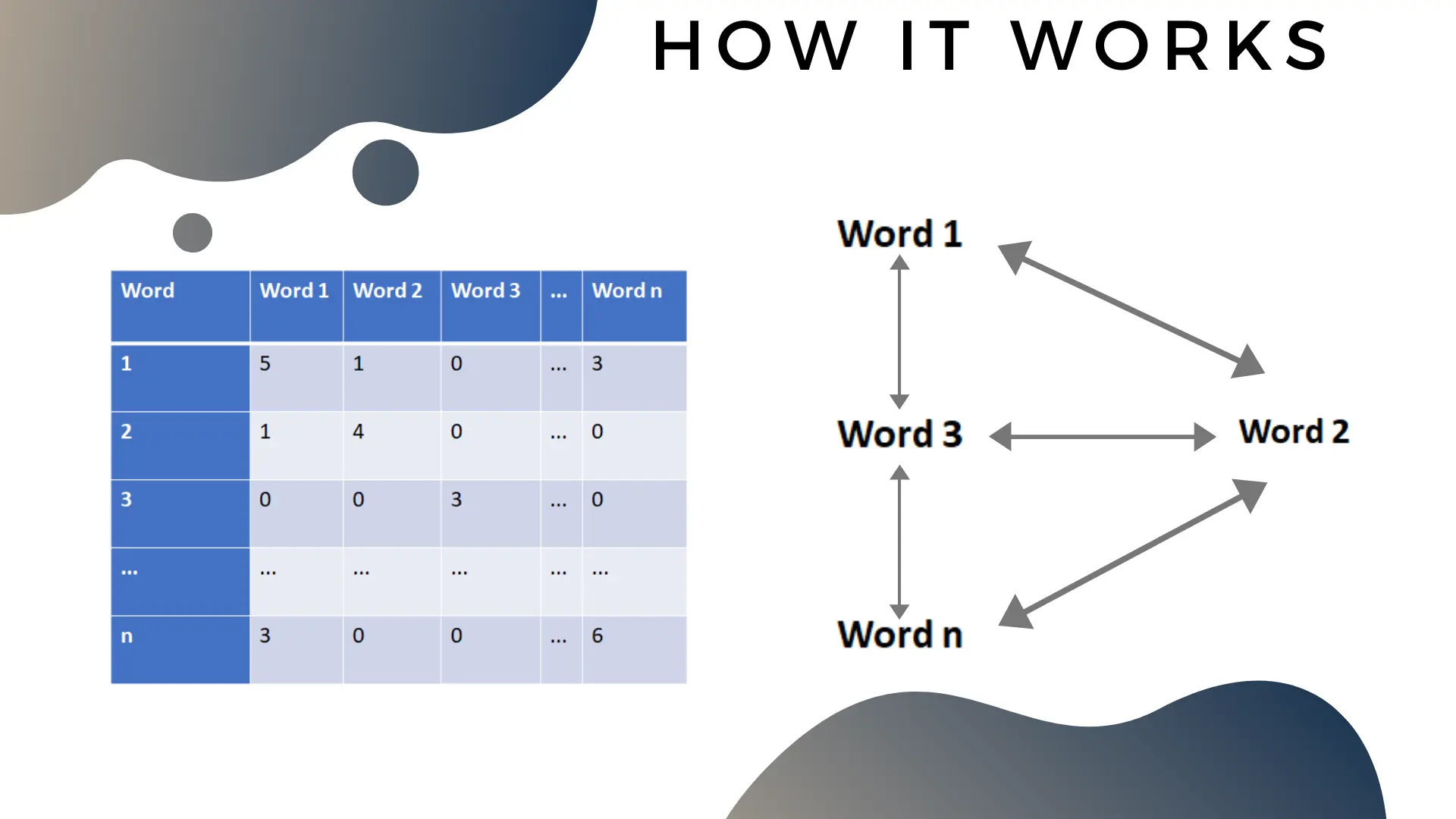
Almost all embedding methods, whether it’s on words, social networks, chemical compounds or other objects will be fundamentally doing two operations:
Compressing a matrix
Destroying a graph’s hard structure and replacing it with a soft coordinate system
The two operations are actually the same operation, and they happen at the same time, because the graph and the matrix are different views on the same abstract mathematical object.

The simplest way to think of word embedding is that they’re simply a dense and compressed version of the full word co-occurence matrix. In fact, the most popular word embedding methods are doing this matrix compression in a roundabout way: GloVe works directly on the co-occurence data. Word2Vec instead uses a tiny neural network to compress co-occurence relationships efficiently.
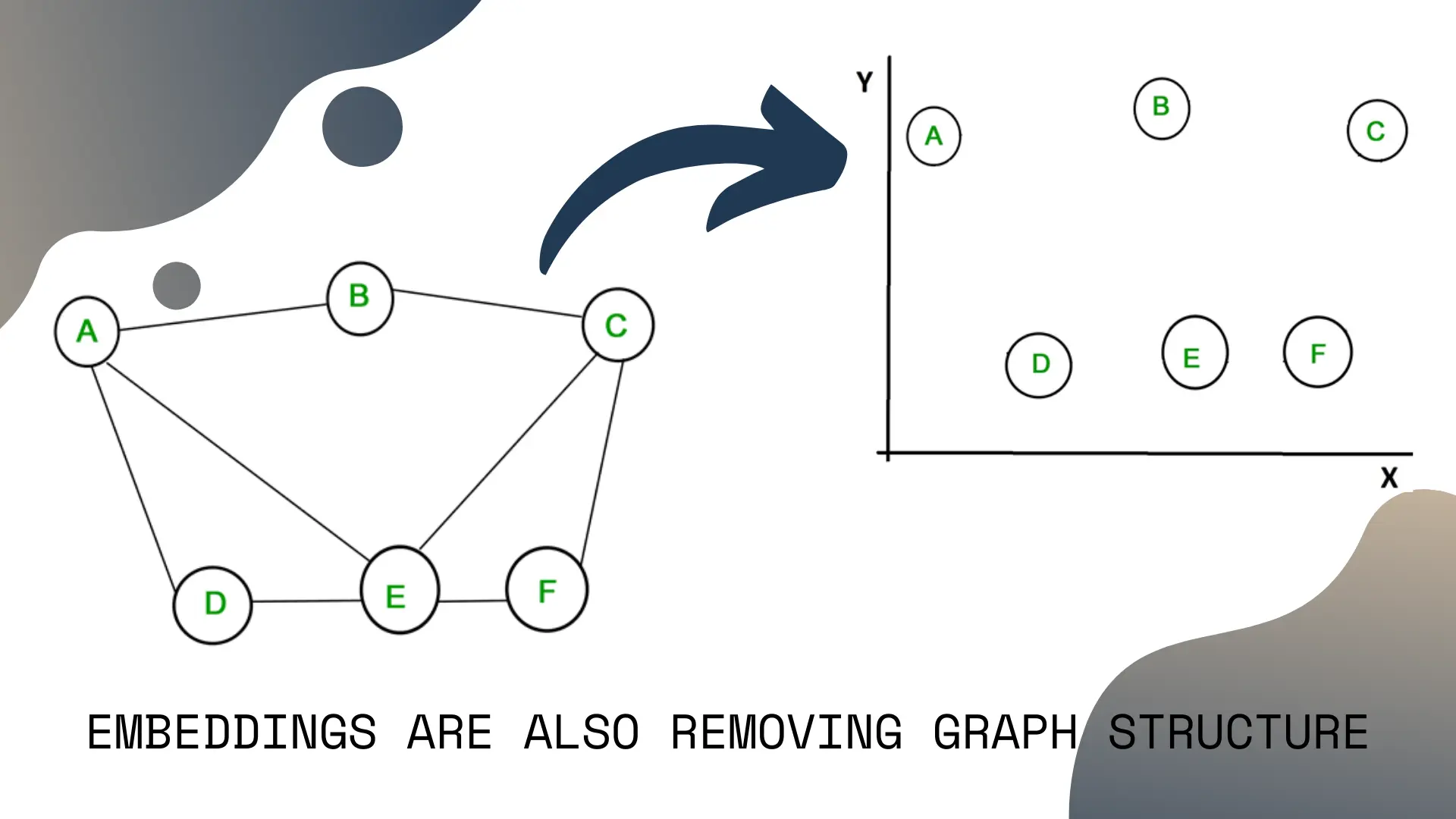
The other way to think of embeddings is that we’re taking a graph, removing the hard structured relationships, and replacing it with a soft coordinate system.
This line of thought is not that relevant for word embeddings, but it’s important to keep in mind, because in a few minutes we’ll be looking over more exotic uses, like embedding the Instagram social network.

If embedding is such a simple idea, why did it only become popular in the 2010s?
The main reason seems to be scalability. For word embeddings to be useful, they need to be trained on huge amounts of text, and it’s effectively impossible to work with the full co-occurence matrix at that scale. Methods like Word2Vec and GloVe add a bit of complexity to the training process, but bypass holding the full co-occurence matrix at once, which lets us scale up the amount of data we’re training on.
Network embeddings
Because embedding methods naturally create embeddings for graphs, the next most popular use is network embeddings. Here, instead of working on the entire network, we represent any node in the network by its embedding vector, and operate on that instead.
This bypasses a lot of practical issues you run into with large networks – instead of operating on the full scale network at all times, we only care about a single node and its small vector of numbers.

One popular method to train embeddings on large networks is the DeepWalk/Node2Vec method. We take a large amount of random walks on the graph, and treat those random walks like an analogue to “sentences” in word embeddings. Then we do the rest of the training the same way.
Sidenote: I maintain a fast python implementation for Node2Vec embedding NetworkX graphs here which I encourage you to use for graphs that fit on your computer [footnote]Another good method for smaller graphs is using UMAP on the graph’s transition matrix. Just normalize the graph’s matrix and throw UMAP at it [/footnote].
Case Study: Instagram’s “Explore” Page
Network embeddings are useful because they allow you to ingest network relationships into downstream machine learning models. This effectively bridges the discrete graph mathematical world where your network lives with the linear algebra mathematical world which machine learning models live in.
Instagram, for instance, maintains “Instagram2Vec” social network embeddings for all their users. This is the building block for their core recommendation system architecture:
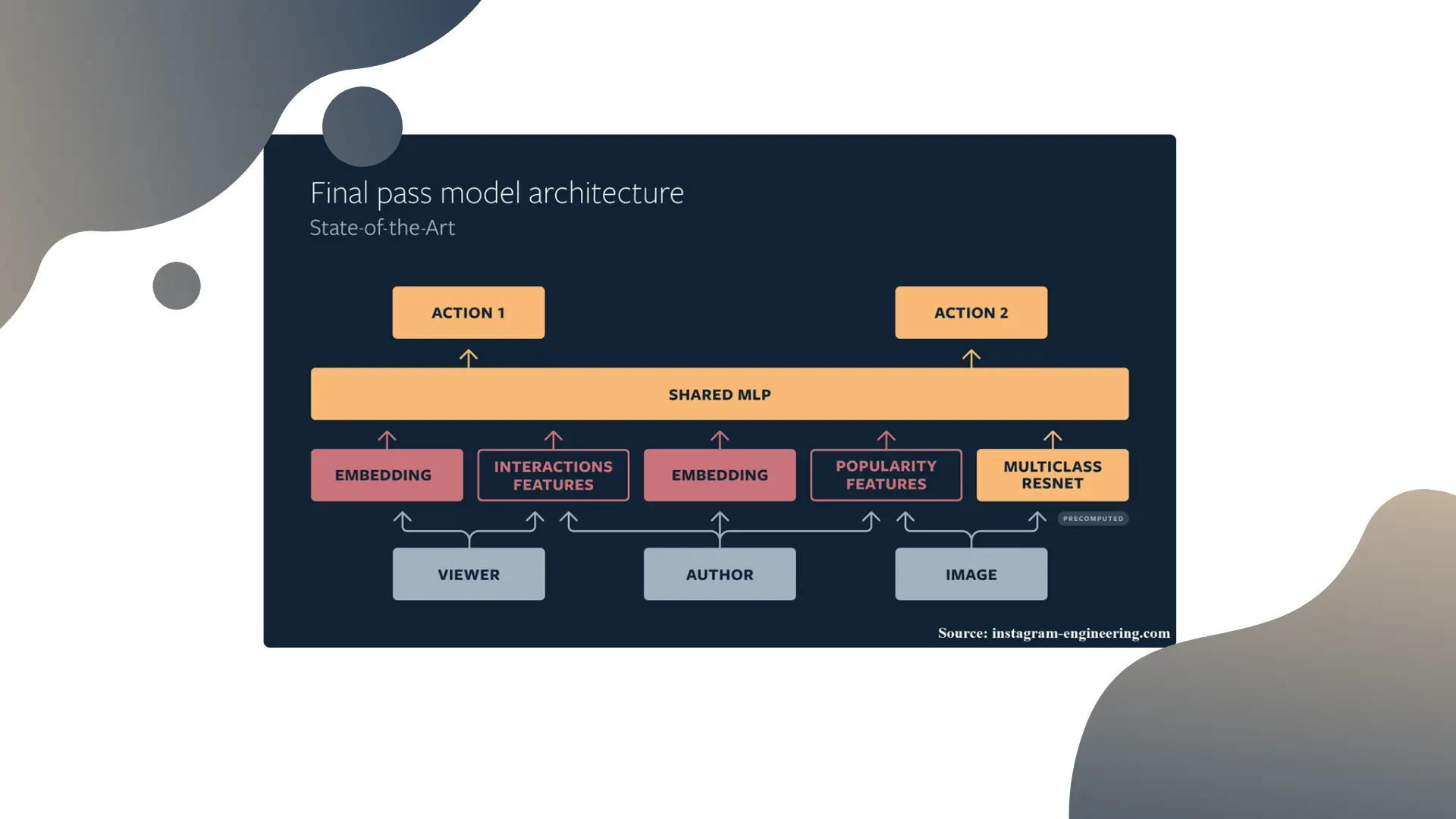
The model recommending the pretty pictures on the Instagram explore page uses the user and the author’s network embeddings, with additional features, and ingests them in a straightforward neural network to generate predictions (see the linked post for more details).
When you should use embeddings
The most common use for embeddings is when you have an object that you want to do mathematics on but isn’t part of any number system. Word embeddings fall into that category.

An other reason to use embeddings is that doing optimization on the real numbers is generally much faster than doing optimization on discrete numbers [footnote]AKA the power of gradient descent [/footnote].
One general theme across computer science is that optimization on discrete objects tends to be hard while optimization on continuous numbers is fast. Sometimes, accepting a lossy but efficient solution is the only way to make a problem tractable.
Sometimes, the structure of the problem space itself makes it impossible to solve without first transforming the problem space itself. An analogy for that is trains versus self driving cars.

Trains work on a well engineered problem space. It’s easy to automate a train’s normal operations, because most relevant inputs and outputs related to driving a train car can be accounted for and worked with.
On the other hand, road networks have a messy and inconsistent structure. This makes it very hard to automate road driving tasks, because almost nothing related to driving can be expected to be a reliable signal. This lack of reliable structure is why recent self driving car breakthroughs generally use neural networks working directly on LIDAR and camera inputs: the only way to build a working system is to work the loosest possible input signal structure.
For more common business use, it’s normal for a data science project to be started on mature software products, where the database structures are built for to support CRUD operations rather than data science or analytics tasks.
Most poorly managed data science (in my experience) teams fail to perform because they work on data structures that aren’t built for what they’re trying to do. For a data science team to perform well, they either need to create structures that support what they want to do (often a large and costly data engineering project up front). That said, sometimes, it’s possible to bypass the bad database structure with methods like embeddings to more quickly accomplish what the data science team was initially trying to do.
Under the hood
Most people treat the numbers in embedding vectors as magic black boxes. Jay Alammar explored the content of the embedding themselves and his visualizations show how the content can represent meaningful concepts.
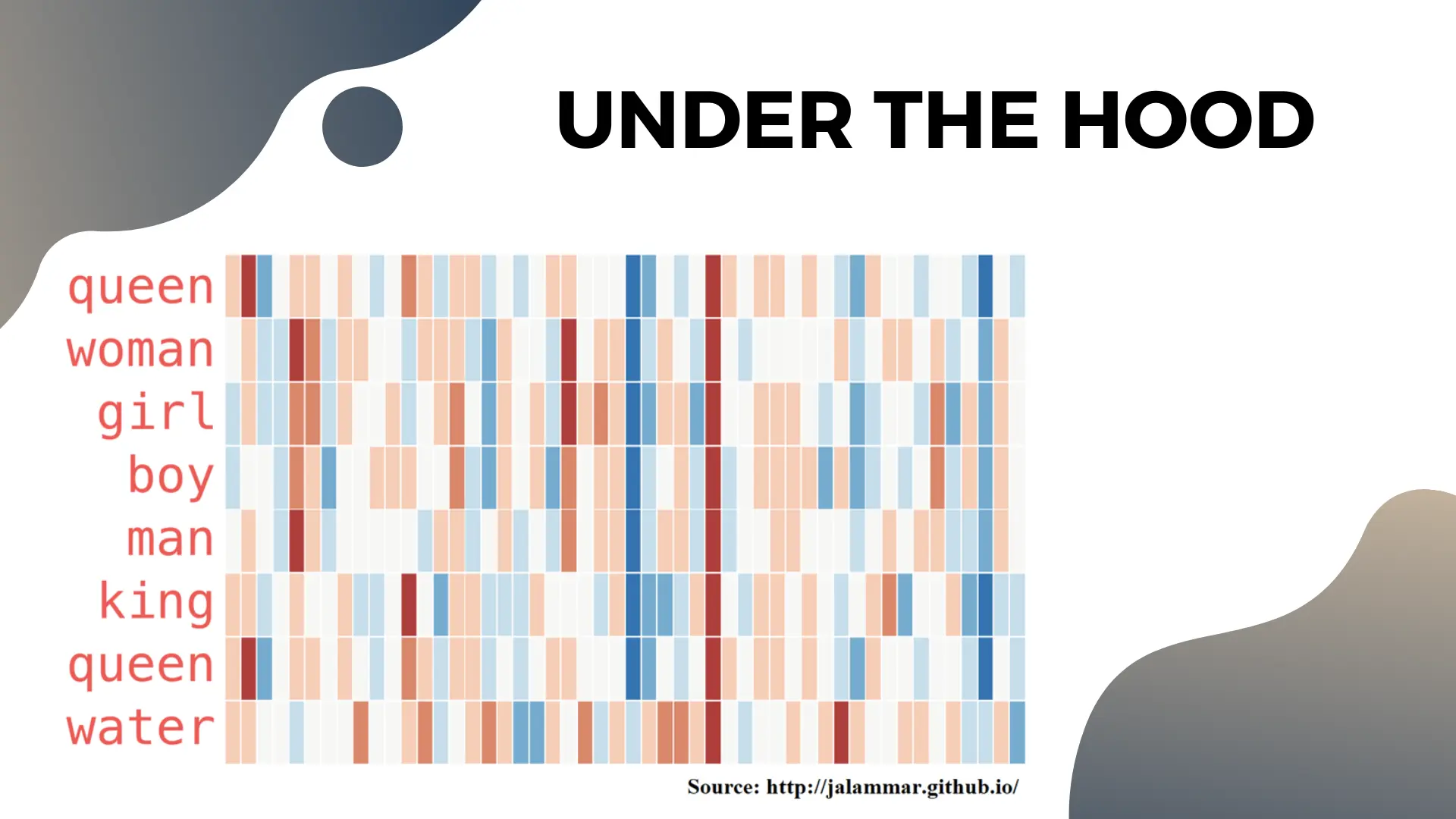
Here, the vectors’ numbers are encoded as a color gradient, with negative values being blue and positive values red. Notice the dimension towards the middle seems to encode personhood, as all words except “water” have large negative values for it. Similarly, the 12th dimension from the left seems to capture some concept of monarchy as they appear larger for “king” and “queen” than any other word.
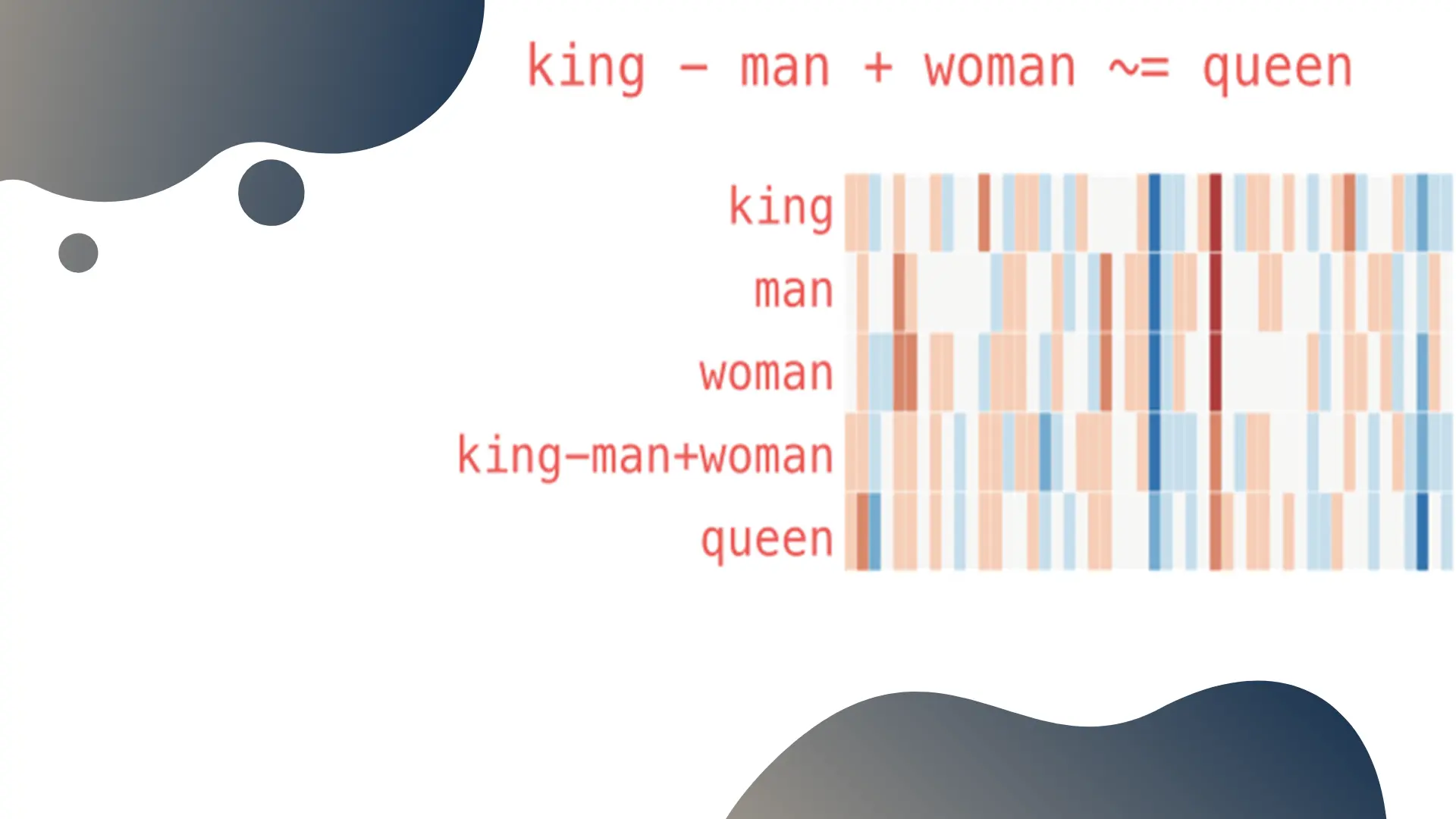
We see how algebra on words will function if the human-level concepts we’re doing algebra with are captured in the embeddings’ vector dimensions.
The math of embedding vectors
Much like matrices and graphs, statistics and geometry have a deep connections to each other.
One of the basic connections is that data can be represented as vectors, and that measuring the angle between the vectors is the same as measuring the correlation. Vectors that are at 90degree to each other are “orthogonal”, or perfectly uncorrelated.
If we’re compressing a matrix from 2m columns to 50 columns, the 50 dimensions in the resulting vector space should (hopefully) capture the most important statistical relationships in the data. These concepts will “separate out” to basis vectors each at 90degrees from each other, which will maximize the efficiency of the new smaller set of dimensions.
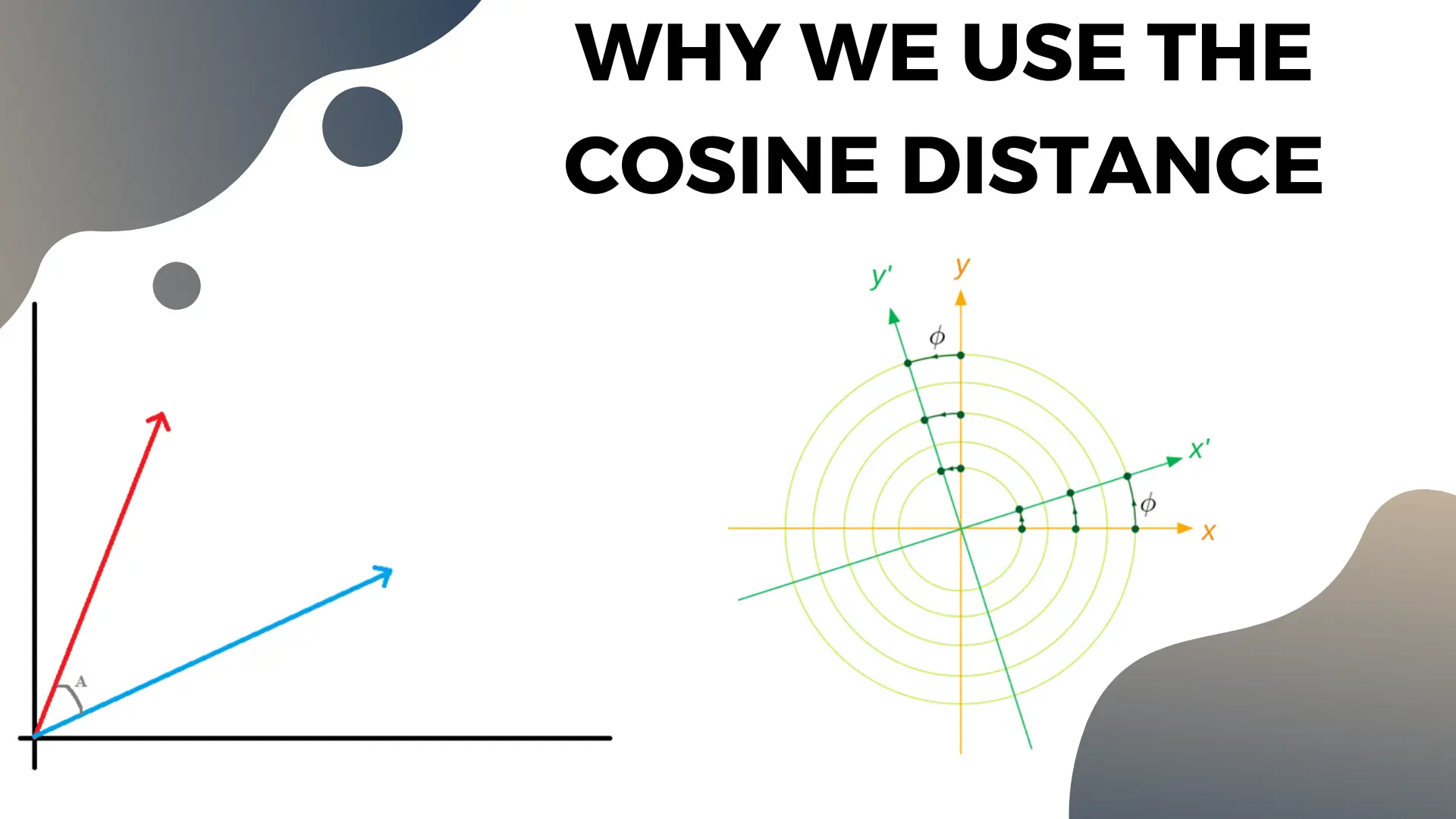
Note that nothing we said above guarantees the embedding vectors’ dimensions will be the meaningful basis vectors that represent the abstract human concepts. It’s possible (read: overwhelmingly likely) that the basis vectors are “rotated” (like in the right hand image in the slide), so concepts won’t necessarily plot cleanly to specific dimensions like they did in the “personhood vs water” example above.
This is one of the reasons we use the cosine similarity to measure the relationship between different words’ embedding vectors. Cosine similarity measures the angle between vectors, which measures how related they are.
Naive methods of vector distance will fail because the length of the raw embedding vectors generally encodes the popularity of the word in the raw data instead of the meaning [footnote]Remember the diagonal in the co-occurence matrix encores frequency, so common words will have large values and hence “big” vectors[/footnote]. So the euclidean distance between a commonly used word and its uncommon synonym might be high even though they have the same meaning. The angle between those vectors would be small regardless of their length, however.
Testing Embedding models
Unsupervised learning tasks, in general are hard to test. Because we don’t have a readily available test set with ground-truth values to measure performance on.

The lazy way to test an embedding model you built is just to throw its output at whatever downstream task you’re trying to accomplish. Are you building social network embeddings to recommend users things to click on? Then add the embeddings to the recommendation model and measure the improvement in recommendation performance! Clearly if they help downstream performance, then you’re doing something correctly.
The more principled way to test the embeddings generally requires building a handcrafted testing dataset. This requires knowledge on the original data – for words you can build a list of synonyms, and assert that they’re closer to each other than to other random words. You can also do similar test with the output of algebraic relationships (king - man + woman ~ queen), or clustering (build lists of related entities, and assert that the embedding vectors cluster around them).
Normalizing vectors to unit length is a good habit
We talked about taking the cosine distance earlier, because it captures well the the notion of relatedness between two vectors. However, some software packages take offense to the cosine distance as it’s not “proper metric”. This can lead to some annoyances.
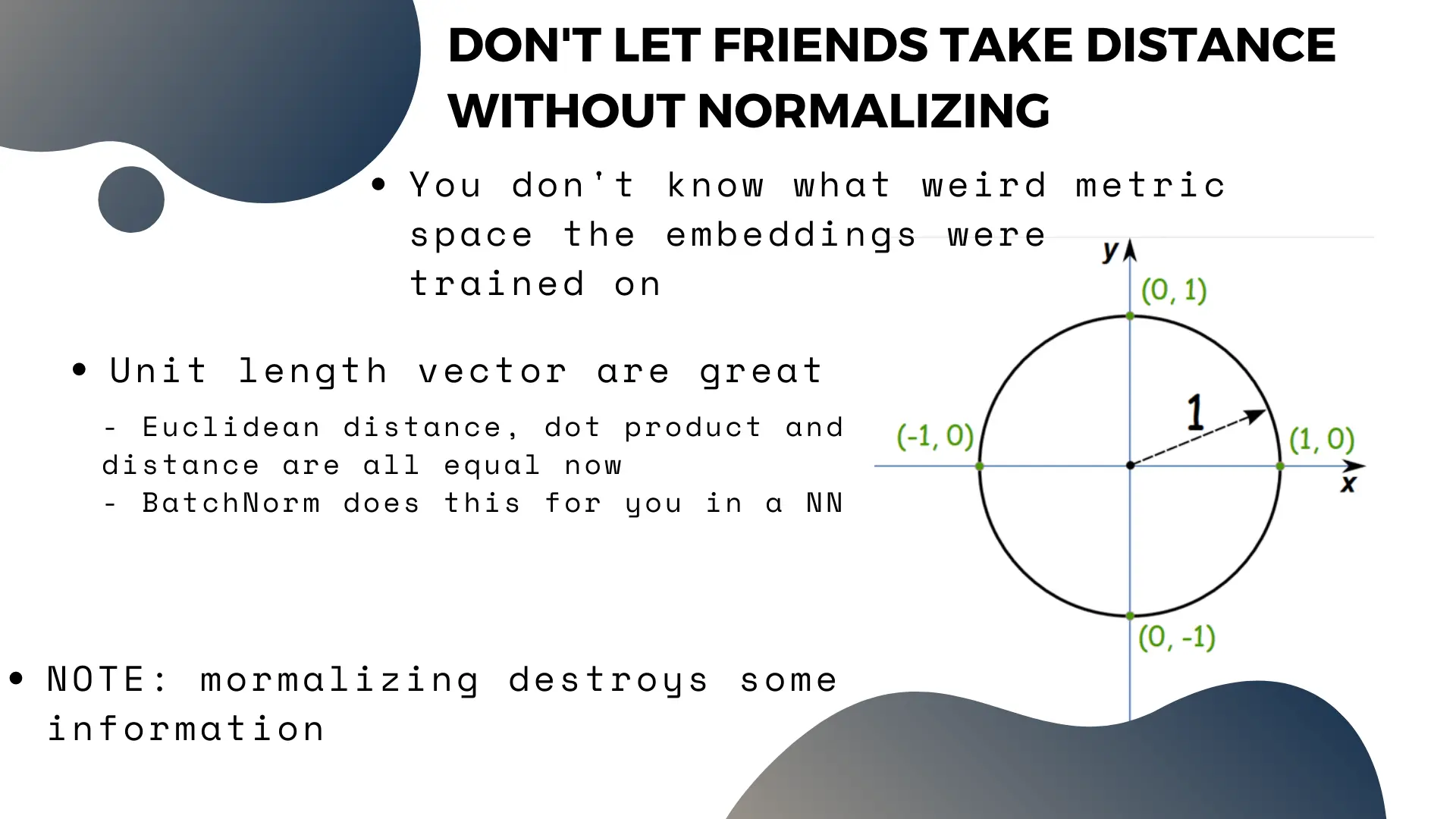
By normalizing vectors to unit length, the cosine distance, dot product and euclidean distance all become the same thing. So before doing anything that involves calculating similarity or distance between embedding vectors, you should consider normalizing them. Think of it like washing your hands, it’s good clean practice.
The one problem with normalization is that it destroys some of the information encoded in the original vectors: the magnitude, which we saw encoded some information on total frequency. So it should be done as far down the pipeline as you can. If you are using a neural network downstream, a batch normalization layer will do this for you, so it’s fine to keep raw vectors all the way down your data pipeline up to the neural net.
Aggregating embeddings
We went over the concept of word embeddings, but what if you want to embed a sentence, or a Wikipedia article?
Your first go-to should be to aggregate the embeddings of the words. There are some more complex methods, but they generally don’t perform better than straightforward aggregation methods. As a general rule, be very skeptical of any individual machine learning papers claiming their very complex methods beat simpler methods on some baseline task.
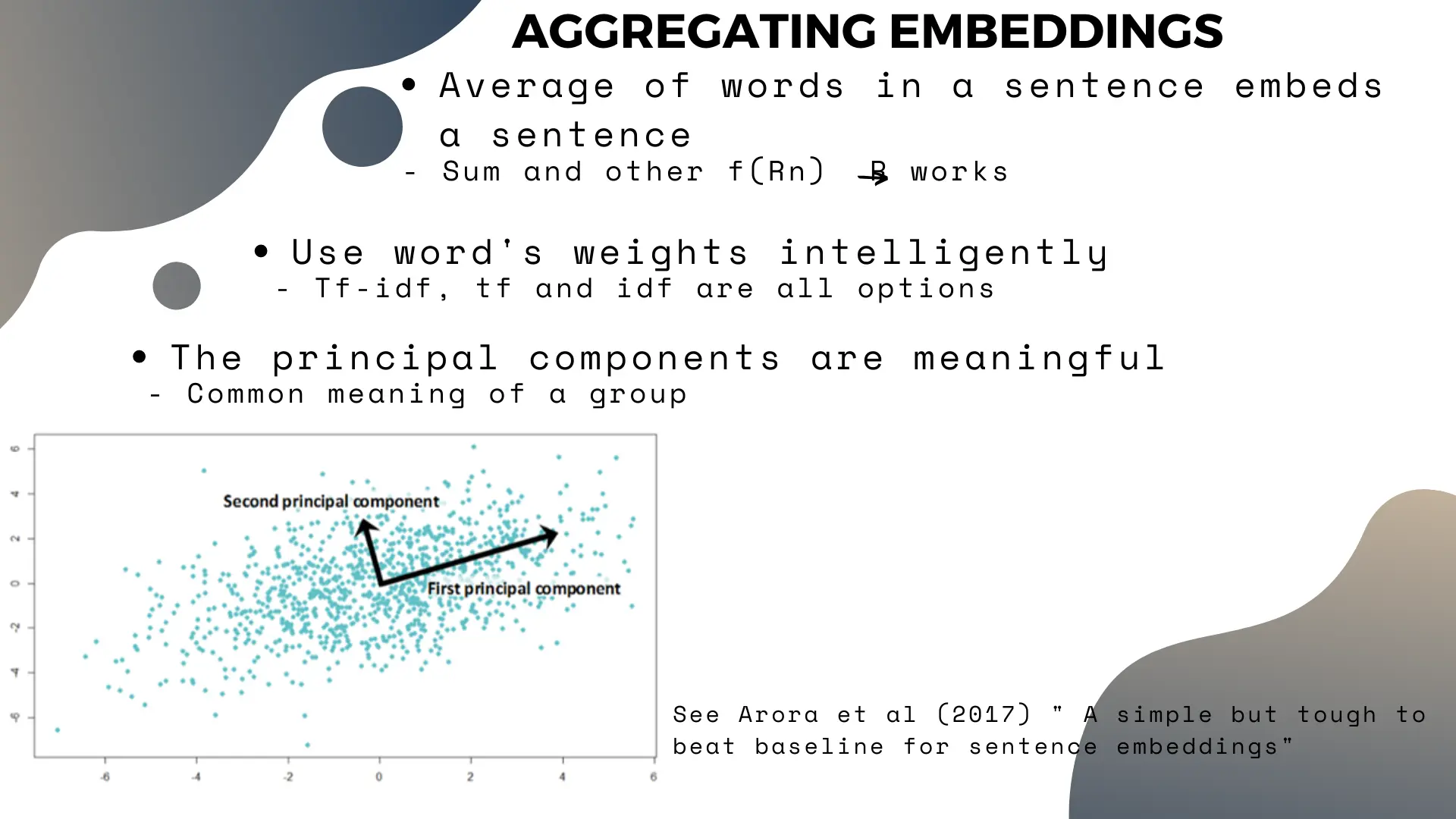
Some simple methods, like averaging or summing all the words in a sentence, tend to work well. The one caveat is that you should use weight individual words for the sum or average operation, and that these weights should be carefully considered depending on what you aim to achieve.
For normal tasks, the inverse of the word’s overall frequency is a good baseline (since uncommon words tend to carry more meaning in a sentence). Other methods like TF-IDF may also work, depending on what you think is important in your task.
Another useful trick is to note that the first principal component of the embeddings of words in a sentence, or the sentences in a paragraph, will pick up the “common theme” between those words/sentences. This makes sense if we think back to the “math” section above – the first principal component should be the most relevant basis vector.
So removing the first principal component from a matrix of embedding vectors might help “clean up” your data. For instance, if you have a pile of legal text which you want to cluster by topic, removing the first principal component could remove the “law” topic, leaving only the more meaningful differences between the different documents in the embeddings.
Multi Language Embeddings
Let’s imagine we train an embedding model on all of English and French wikipedia articles at once.
If we think back to the word co-occurence matrix and graph, then the English and French words should never appear together in a sentence. So the co-occurence graph will have two large clusters (one per language).
This also means the embeddings of translated synonyms (eg. “House”, “Maison” and “Casa”) will be very far apart in our model, since they’re on different “islands”, even though their meaning is the same.
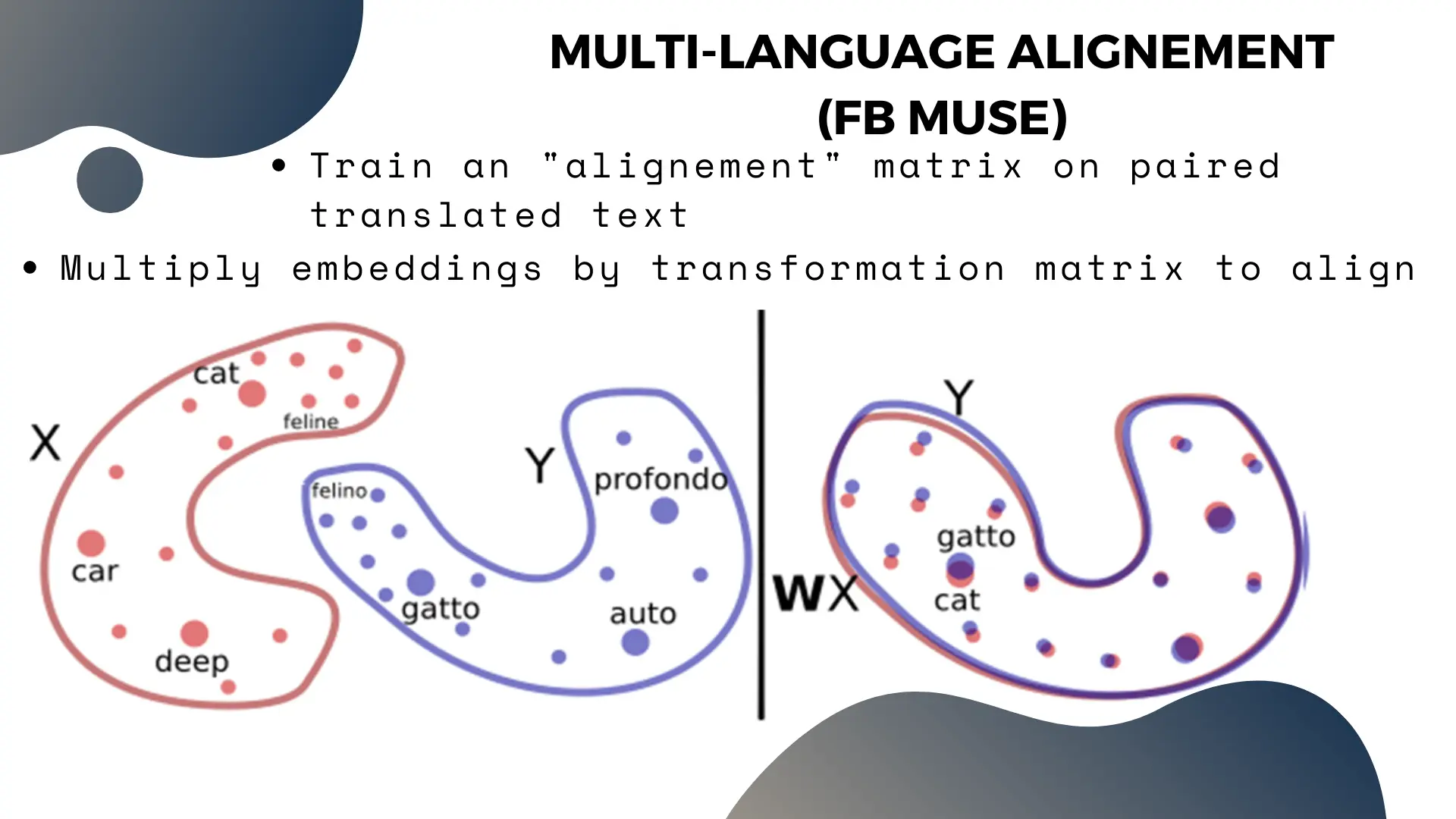
The solution to this problem is to “align” the vector spaces together.
The basic technique is to create a dataset of translated pairs of words, and train an “alignment matrix” which solves the equation that aligns their vectors. Then, we can multiply the embedding vectors by that matrix to align the entire language’s vector space to the other.
Language Model Embeddings AKA “You probably don’t need BERT”
One problem with normal word embeddings “polysemy”, where a word written the same has a different meanings depending on context. For instance, “turkey” can both refer to a kind of bird, or to a country.

For advanced applications, full-scale language models (which aim to predict a word given its context) can solve this problem. Like in Word2Vec, the language model will have an internal vector representation of the word, which we can use as the embedding. The advantage of a language model is that this representation changes depending on the context around the word, unlike the embeddings we’ve seen before.
Language models like GPT-2 and BERT don’t encode any sort of understanding of human language (regular word embeddings don’t either for that matter). Read the linked sources for more information on this topic. However, language models do perform well at reproducing the statistical patterns of human language.
Because a full scale model like BERT has a different embedding for a word depending on its context, the embedding is robust to problems like polysemy, and arguably has higher quality embeddings for common words.
That said, here’s a rule of thumb: If you’ve read this article up to this point, you don’t need BERT for your embeddings. If you’re working on a NLP task that legitimately requires BERT, you’d have gotten bored by this introductory material and stopped reading already. For common vanilla uses of embeddings, you generally don’t need BERT.
While our previous embedding models take some work to train from original data, once they’re trained they’re effectively a static map word -> vector. This is very fast and efficient to work with. Working with BERT to get embeddings, on the other hand, is cumbersome and computationally expensive. Moreover, it requires more complex coding to extract contextual embeddings, whereas it’s a one line affair with regular embedding libraries like Gensim.
All of this effort is not even guaranteed to produce significantly better results for your downstream task! Does your data depend heavily on sentence context? If it seriously does, I encourage you to try BERT, after you accomplished it with simpler embedding methods.
Conclusion
Embedding methods will be one of the foundational method in any qualified data scientist’s toolbox. While they’re incredibly useful in NLP, they’re also useful in all sorts of other contexts, because the real numbers are simply a friendly neighbourhood to work in.
If you have questions, or want pointers for an embedding project you have, feel free to email me or message me on twitter.
